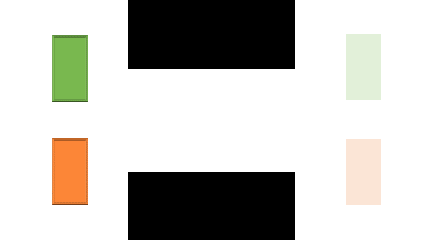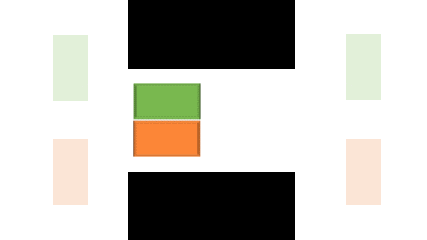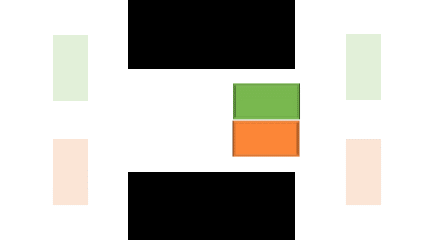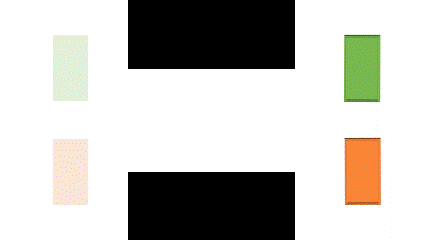About Me
Undergraduate at Texas A&M University @ College Station. Computer Science / Applied Math Double Major. For more about me, you can visit my website.
About My Mentor
Nancy M. Amato is Regents Professor and Unocal Professor of Computer Science and Engineering at Texas A&M where she co-directs the Parasol Lab and is Senior Director of Engineering Honors Programs. In January 2019, she will join the Department of Computer Science at the University of Illinois at Urbana-Champaign as Department Head and as Abel Bliss Professor of Engineering.
Amato received undergraduate degrees in Mathematical Sciences and Economics from Stanford, and M.S. and Ph.D. degrees in Computer Science from UC Berkeley and the University of Illinois, respectively. Her research focuses on motion planning and robotics, computational biology and geometry, and parallel computing. She has graduated 23 PhD students, with most going to faculty positions in academia (10) or research positions in government, industry or academic research labs (10). She is VP for Member Activities for the IEEE Robotics and Automation Society (RAS), served as program chair for the 2015 IEEE International Conference on Robotics and Automation (ICRA) and for Robotics: Science and Systems (RSS) in 2016. She is an elected member of the CRA Board of Directors (2014-2020), was an elected member of the RAS AdCom (2009-2014), was co-Chair of CRA-Women (2014-2017) and of the NCWIT Academic Alliance (2009-2011).
Amato received the 2017 RAS Distinguished Service Award, the 2014 CRA Habermann Award, the inaugural NCWIT Harrold/Notkin Research and Graduate Mentoring Award in 2014, the 2013 IEEE Hewlett-Packard/Harriet B. Rigas Award, and Texas A&M university-level awards in teaching (2011) and research (2018). She is a AAAI, AAAS, ACM, and IEEE Fellow.
About My Project
Background
Motion planning (MP) problems are defined as finding a motion a robot can take from point A to point B in a continuous workspace without colliding with obstacles. Naively searching the entire continuous space is intractable because of the time required to check each configuration’s validity is relatively high, so algorithms such as Probabalistic Roadmaps (PRMs) take samples of configurations to try and find from sample to sample. For these problems and similar problems, we care about completeness (will it find a solution if there is one) and optimality (will it find the best solution by some metric, e.g. distance). Some PRM variants address these two points by showing they are reached asymptotically, while others may be suboptimal or incomplete but have faster run time or other practical advantages.
Multi-agent motion planning (MAMP) is a generalization of MP where there are multiple robots which also must not collide with eachother. The discrete environment version of this problem is multi-agent path finding (MAPF), where each robot occupies a node on a graph and cannot share nodes or cross the same edge with another robot at the same time.
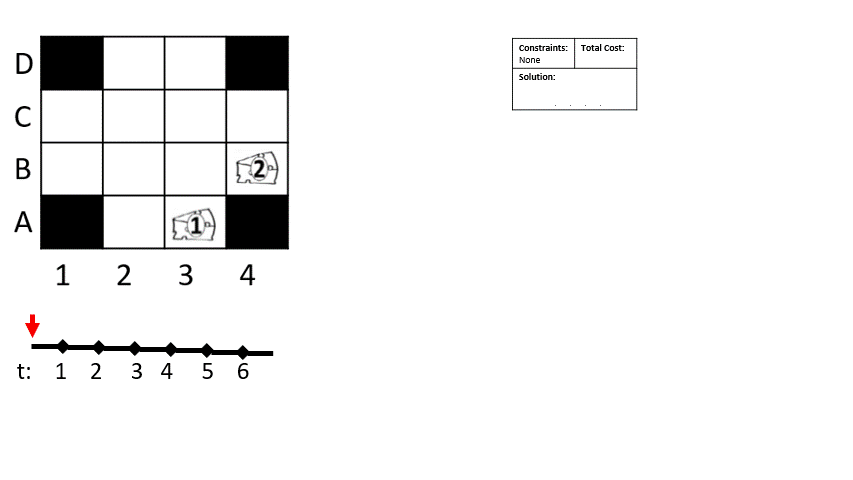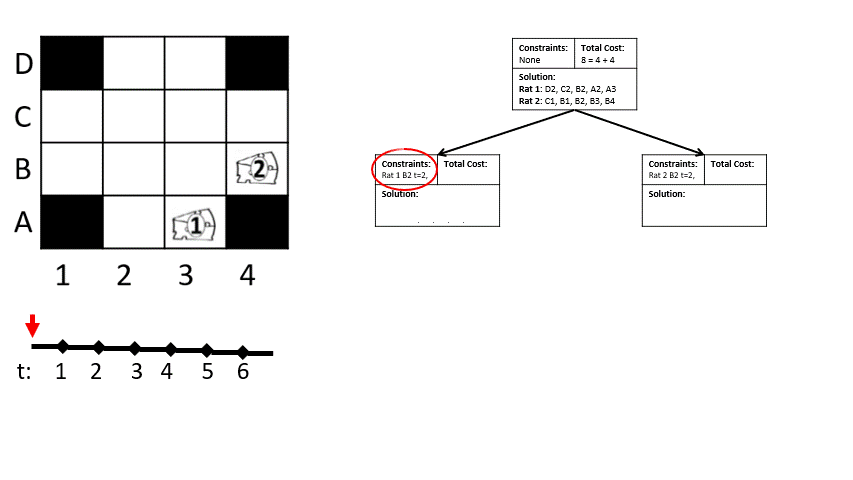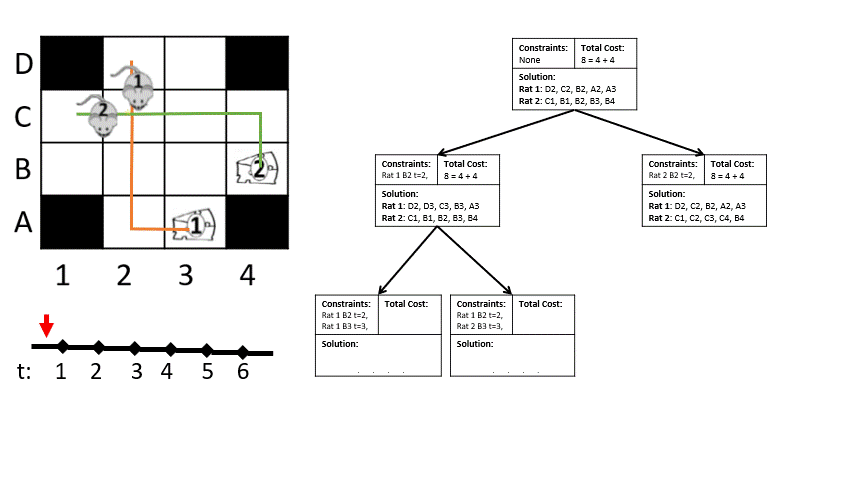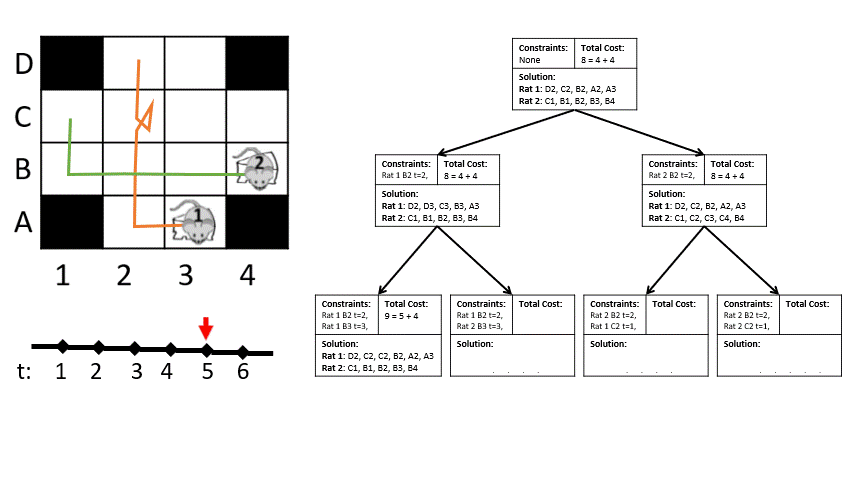
Conflict-based search (CBS) and variants of it have been applied to both these problems with much success. The animation on the left shows the classic CBS problem in a discrete grid with only two robots. The data structure in this animation is the Conflict Tree. For each leaf of the tree, we evaluate it to determine the first conflict between a pair of robots. Two children of this node are created, each one containing an additional constraint that one of those two robots cannot be in that contested tile at that time. Evaluation takes these constraints as dynamic obstacles; these constraints are the only information that robots have about eachother while planning.
Project Description
I am working with Irving Solis on an idea with the working title of Local Template Repair. The idea is to use templates of local interaction to attempt to resolve conflicts locally between robots when possible. Some intuitive templates types include waiting for one robot to pass, moving behind the robot, and aligning with the other robot to fit though a passage. However, the idea seems like it can be generalized to more abstract interactions and situations, and part of the research is exploring that aspect. The expected outcome is to find a generic method that can be applied to MAMP problems which can improve the speed at which sub-optimal paths are found.
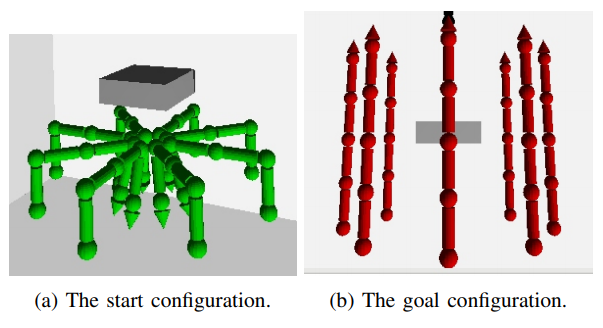
A template is a defined pattern of interaction between two robots, as shown in the cartoon example on the left. In this example, the interaction is that the two robots are trying to move through a narrow passage. This research is will focus on simple rigid body robots like these at first, but aims to lay the groundwork for more general template repair.
The templates can then be applied by transforming it with a set of operators and/or constraints into a valid position. Part of the research includes figuring out how to applied these, and similar problems may be surveyed if no feasible trivial method is found. In our implementation, we will be applying and testing these methods in the CBS-MP algorithm described in Representation-optimal multi-robot motion planning using conflict-based search, which is an exisiting MAMP solver that uses PRMs in an extension of CBS. In our usage, templates will be applied to try and resolve conflicts, and default to existing methods if no local template repair can reasonablt be found.
Our method provides advantages over existing techniques. In CBS and all of its current variants known to us, globally replanning can be used to resolve a conflict; meaning that all robots redo their entire individual motion planning but while avoiding that conflict. Our method applies only locally (both temporally and in robots involved), so it scales better when there is many conflicts and robots. Our lab is also working on performing local repairs by locally resampling and locally replanning; templates require this planning component to be done only once per template regardless of number of conflicts. By only generating the motion planning once rather than each repair, the runtime of these repairs motion planning is constant, which allows the usage of slower, better quality algorithms more likely to find local solution, or find a local solution is closer to optimal.
Final Report
View my final report by clicking here.